기초적인 조명셰이더(2)_정반사광specular light

난반사광diffuse light에 이어 정반사광specular light에 대해 알아보겠다

 

정반사광specular light란?

난반사광과 달리 한 방향으로만 반사되는 빛으로 입사각이 출사각과 같은 것이 특징이다.

 

게임업계에서 널리 사용하는 기법인 퐁phong 모델을 사용해보겠다.

퐁 모델은 반사광과 카메라벡터(카메라에서 현재 위치까지 선을 그은 벡터)가 이루는 각도의 코사인 값을 구하고,

그 결과를 여러번 거듭제곱하면 정반사광을 구할 수 있다고 한다.

 

거듭제곱을 하는 이유는?

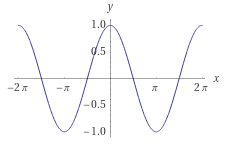
거듭제곱수가 늘어남에 따라 코사인 값이 빠르게 줄어드는데

정반사광의 폭은 난반사광에 비해 상당히 타이트하므로 이를 재현하기 위해 코사인 값에 거듭제곱을 한다.

y = cos(x) 코사인 그래프

y = cos(x)^2 거듭제곱 코사인 그래프

 

정반사광을 구현하기 위해 반사광 벡터와 카메라 벡터가 필요한데

반사광 벡터는 기존 입사광 벡터에서 구할 수 있고 카메라 벡터를 구하기 위한 float4 위치 전역 변수를 만든다.

ViewPosition 변수 시맨틱을 대입한다.

정점셰이더 Vertex Shader

float4x4 gWorldMatrix;
float4x4 gViewMatrix;
float4x4 gProjectionMatrix;

float4 gWorldLightPosition;
float4 gWorldCameraPosition;

struct VS_INPUT 
{
   float4 Position : POSITION0;
   float3 Normal : NORMAL;
};

// 정반사광을 구하려면 코사인 값에 거듭제곱을 해야 하는데
// 거듭제곱을 한 뒤 보간을 한 결과와 보간을 한 뒤에 거듭제곱을 한 결과의 차이는 엄청나므로
// 정반사광 계산은 픽셀셰이더에서 한다.
// 계산에 필요한 두 방향벡터인 R과 V를 구한 뒤에 픽셀셰에더에 전달해 주도록 한다.
struct VS_OUTPUT 
{
   float4 Position : POSITION0;
   float3 Diffuse : TEXCOORD1;
   float3 ViewDir : TEXCOORD2;
   float3 Reflection : TEXCOORD3;
};

VS_OUTPUT vs_main( VS_INPUT Input )
{
   VS_OUTPUT Output;

   Output.Position = mul( Input.Position, gWorldMatrix );
   
   float3 lightDir = Output.Position.xyz - gWorldLightPosition.xyz;
   lightDir = normalize(lightDir);
   
   // 입사광의 방향벡터를 구했던 방법과 동일하게 카메라 벡터를 구한다.
   float3 viewDir = normalize( Output.Position.xyz - gWorldCameraPosition.xyz );
   Output.ViewDir = viewDir;
   
   Output.Position = mul( Output.Position, gViewMatrix );
   Output.Position = mul( Output.Position, gProjectionMatrix);
   
   float3 worldNormal = mul( Input.Normal, (float3x3)gWorldMatrix );
   worldNormal = normalize(worldNormal);
   
   Output.Diffuse = dot(-lightDir, worldNormal);
   
   // 반사벡터는 reflect()라는 함수를 사용하여 구한다.
   // 입사광의 방향벡터와 반사면의 법선을 인자로 받는다.
   Output.Reflection = reflect(lightDir, worldNormal);
   
   return( Output ); 
}

 

 

픽셀셰이더 Pixel Shader

struct PS_INPUT
{
   float3 Diffuse : TEXCOORD1;
   
   // 정점셰이더의 출력데이터에서 가져올 두 벡터를 추가한다.
   float3 ViewDir : TEXCOORD2;
   float3 Reflection : TEXCOORD3;
};

float4 ps_main(PS_INPUT Input) : COLOR0
{   
   float3 diffuse = saturate(Input.Diffuse);
   
   // R과 V를 다시 정규화해준다
   // 그 이유는 보간기를 거치는 동안 그 값이 흐트러질 수 있기 때문이다.
   float3 reflection = normalize(Input.Reflection);
   float3 viewDir = normalize(Input.ViewDir);
   float3 specular = 0;
   
   // 난반사광이 존재하지 않는 표면에는 빛이 닿지 않으므로
   // 정반사광이 존재할 수 없다.
   // 하여 난반사광의 양이 0%이상일 때에만 정반사광을 계산한다.
   if(diffuse.x>0)
   {
      // 두 벡터의 내적을 구한 뒤, 거듭제곱을 한다.
      specular = saturate(dot(reflection, -viewDir));
      specular = pow(specular, 20.0f);	// 20번 거듭제곱을 한다.
   }
   
   // 빛이 없는 부분이 칠흑같이 어두우므로 간단하게 주변광을 정의해 조금 밝혀본다.
   float3 ambient = float3(0.1f, 0.1f, 0.1f);
   
   return float4(ambient + diffuse + specular, 1.0f);
}

 

 

diffuse light + specular light + ambient

픽셀 셰이더의 결과값을 return float4(specular, 1.0f);로 바꿔 specular의 값만 확인할 수도 있다.

ambient 값이 없는 모습 빛을 받지 않는 부분은 너무나 어두워 보이지도 않는다.

거듭제곱의 횟수를 의미하는 float형 전역변수를 만들어서 specular의 값을 실시간으로 변경해서 확인할 수도 있다.

출처 : 셰이더 프로그래밍 입문